In low-informed exploratory robotics (low-informed), it is often overlooked that both intrinsic and extrinsic factors can influence the effectiveness and uncertainty of search strategies. We report here the impact of these factors on the effectiveness of random searches using the metrics discussed in the previous section.
Search for diffusivity parameters.
The motion pattern for a random search strategy can also be described as a series or displacements that travel in different directions. Lvy Search, a superdiffusive strategy that defines the length and probability distribution of these travels, is a good example. There are many options for (alpha)The search diffusivity is defined in the Robot simulation models section. Robotics is a complex field that can cause deviations from the theoretical distributions. This can affect the outcome of a particular choice. (alpha) parameter. Extrinsic factors, such as energy limitations and motor plant drift, can often lead to a reduction or modulation in search diffusivity. This is illustrated in Figure.2.
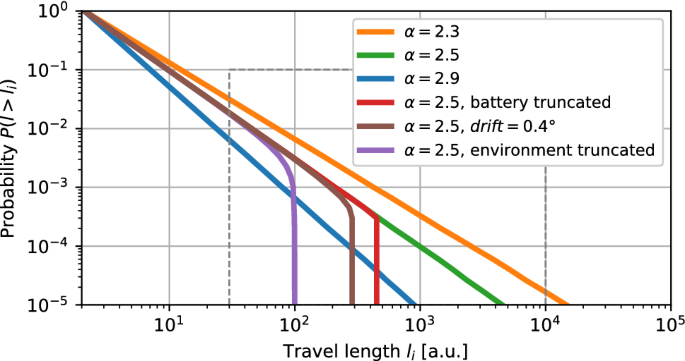
Modulation of Lvy travel duration probability by intrinsic or extrinsic variables. Each trace represents the complementary cumulative distribution function, (CCDF), of the travel lengths for each strategy/parameter combination. We show its modulation using the exponent parameter (alpha)(blue traces, orange traces, and under different factors): intrinsic (battery-truncatedredanddrift boundbrown) and external (environment bound), a basic model that truncates tracks at (10^2) a.u. to denote the search area diameter limitpurple trace Each CCDF was calculated numerically using the Robot simulation models section. The dashed rectangle represents the region used for battery and drift analyses discussed in Figure.
The modulation of Lvy parameters is illustrated in Fig.2. (alpha). A large value (alpha) ((>3)A search strategy driven by model (2) would result in searches that are shorter and eventually converging into a Brownian movement implementation. A lower value (alpha)The overall diffusivity of Lvy searches is increased, and this serves as a baseline in our study. (alpha)Parameter was set to 2.5
Travel paths can also be constrained by intrinsic and extrinsic variables. Travels were cut short by the boundaries and obstacles within the search area in the case of environmental constraints (purple trace in Figure.2). Travel truncation occurs when there is uncertainty in a motor plant. This causes motion drift (brown trace) to distort the linearity and affect diffusivity. In the event of energy restrictions, it is possible to truncate longer trips to avoid having a single motion dominate the statistics. This is illustrated by the battery truncated (red trace, Fig.2) in which travels that exceed 10% of the total energy available are summarily reduced. Theoretical analysis allows you to evaluate each factor separately. In practice, however, these factors often appear together.
In Fig.3, we can see the combined effects of drift and battery constraints. If we start with the battery-truncated case (bright–green trace), and then consider a small amount drift (bright–red trace), it is clear that the differences are moderate. The battery truncation effects mask the drift effects. It is important to consider the effect of drift on diffusivity when it is increased (bright blue trace). In fact, drift is now masking battery constraints’ effect.

Effect of motion drift and battery restrictions on travel length probabilities All traces in this figure (alpha =2.5)There are no environment limits. Lvy search would be implemented strictly according to a power-law (dark green trace). In robot implementation, there are many factors that can affect the strategy. Uncertainty in a locomotive plant (i.e. wheel slipping, inertial sensors accuracy, etc.) can cause motion drift. It effectively limits long distance travel. Two examples of drift values are shown in red and bleu. The battery truncated scenario (brighter red and green traces) is where individual travels are limited in duration to use only 10% of the available battery. (Robot simulation model section).
This analysis can be used to parameterize search strategies. It also allows for efficient decision making about the robot platform itself. For example, it can help determine whether to increase battery range or improve the locomotive plant. This understanding can be used to help design a bioinspired random search strategy, and in particular, when choosing its parameterisation.
Search for area boundaries and obstacles
Environment conditions can be difficult to predict in search problems with high uncertainty. However, it is possible to estimate or partially know in advance issues such as the maximum exploration distance or the presence of obstacles. This knowledge can also be used to define virtual boundaries that limit the search. An a priori understanding can help in choosing a random search strategy.
In this section, we study the effect of the exploration area geometry and the presence of obstacles or inaccessible/forbidden regions. We focused our analysis on the stereotypical set of environments listed in the Search environments section. This set can be used to represent a variety of search situations that are subject to uncertainty. We will examine the exploration diffusivity as well as the spatial and temporal profiles for random search in the subsections that follow.

Exploration diffusivity is the area that each strategy has explored over time. Each trace combines 1000 simulations and represents the minimum area covered at any given time by at least 9000 runs. A square marker indicates the point at which each strategy has covered 85% of the available area (see Table1 to see the area sizes).
Analysis of exploration diffusivity
Different evolutions of the searches can be caused by intrinsic and extrinsic modifications. This is determined by the area that has been explored over time. Random search strategies are stochastic and can make it difficult to determine the representativeness for specific scenarios. To quantify the performance, we considered 1000 simulations for each strategy map combination. Each trace in Fig.4 corresponds with the minimum area covered at any given point in time by 90% of the simulations. This metric corresponds with the timeline for area coverage and allows us to compare the search evolution of each strategy under each map. The square marker that represents the area where each strategy covered 85% is also displayed in Fig.4. We compared the following maps: Plain and Dense Forest, Craters and Sparse Forests, Triangle and Corridor. Then, we ran a set random strategies: Ballistic, Lvy (with memory, mirror bounce and mirror bounce), Brownian (memory ill-informed and memory informed). This particular selection of add-ons was made in order to provide a representative set that could illustrate the concepts discussed in this paper. The software tools can be used to test more combinations for specific problems (Supplementary information).
Fig.4 shows how each combination environment and intrinsic parameters can result in a distinct evolution in search performance. The slow search evolution of the uninformed Brownian search strategy (yellow trace on the panels) is caused by slow search evolution. Ballistic strategies with mirror or random bouncing offer a rapid evolution to cover the searched area (orange traces and blue trace, respectively), which is the best performance for this metric in many map maps. They are not able to perform well in specific environments. Lvy strategies offer intermediate search evolution speeds. A basic memory is included in all maps (grey traces and green traces) to improve the exploration time of both Brownian strategies and Lvy strategies. The corridor map features a unique environment with three distinct regions and narrow passes between. Panel f) shows steps of increasing performance when the robot crosses a passage and explores new areas. The Lvy walk with wall following naturally provides the fastest exploration (pink track) in this case.
The representation in Fig.4 doesn’t provide information about the homogeneity or the nature of exploration for each environment. This makes it difficult to identify, for example, strategies that allow fast exploration of an environment with a desired spatial or temporal profile. This is covered in the next sections.

Heat maps of revisit frequency represent exploration redundancy. They are used to show the frequency of revisits for a variety of search strategies and environment. These panels correspond to:A) Plain map and ballistic random bounce, (b) Dense Forest map and Lvy mirror bounce, (c) craters map and ballistic mirror bounce, (d) Craters map and Lvy mirror bounce, (e) Triangle map and Lvy recast bounce, (f) Corridor map and Lvy wall follow. For each map, representative trajectories have been shown in black(10^4) steps). Additional material includes a video animation, Supplementary Video 1, that shows the evolution and strategies of this metric for Craters map: Ballistic random bounces, Lvy mirror bounces, Brownian without memory and uninformed Brownian.
Analysis of spatial profiles
We used a 2D heatmap representation to compare the effects of environment bounds and barriers over each strategy. This highlights the regions where searches are more frequent. Figure5 shows this analysis. It highlights the spatial profiles of a representative collection of search strategies and environments.
The 2D position grid described under Robot simulation models section was used to perform the analysis in Fig.5. Each grid cell contained the total revisit count. This means that the cell values were kept updated each time the robot’s sensory range was reached. Simulations were run (10^8)Steps were taken to ensure statistical relevance. The resulting heat maps were normalised using the maximum and minimum number of cell visits. This animation shows the evolution of spatial exploration metrics for the Ballistic random bounce and Lvy mirror bounce, Brownian memories, and Brownian strategies.
The heat maps in Fig.5 are the spatial search profile. They indicate the probability of finding the robot at a given location. Time considerations will be addressed in the next section. Panel a corresponds to the Plain search and a ballistic random bounce, where exploration is more prominent near the concave boundary. The convexity and concentration of the 180 is responsible for the higher probability.(^circ)Probability is the probability that the robot will strike the sides of the collision point. (The same effect can also been observed on the Craters map, see Supplementary video 1). Panel b) shows the Dense Forest map with a Lvy mirror bounce search. Despite the complicated map, this strategy achieves highly homogeneous exploration thanks to the Lvy diffusivity combined with the effectiveness and mirror bounce. Panels c and d compare the performance of two strategies on the Craters map. c depicts the ballistic-mirror-bounce search which can cause heterogeneity in the environment. d depicts Lvy mirror bounce strategy where the exploration is uniform (see also Supplementary Video). Panels e), and f) include different geometries. They show the Triangle map with Lvy strategy and recast bounce. There is dense exploration around corners because of the truncation in the Lvy steps upon each collision. Panel f shows the Corridor map with Lvy wall–follow search. This favours narrow areas while allowing for more exploration in the faraway regions.
Depending on how the avoidance and search strategies are implemented, boundary effects can be different. There is less redundancy at the boundaries than there is at the edges (the exception being the wall follow obstacles handler). This is due to the sensor size range. Strategies a) & e) tend to be helpful in certain scenarios. Ballistic strategies can produce fast but non-homogeneous exploration. This is dependent on the environment’s specificities, as shown in panels A and c. Lvy mirror bounce strategies which yielded intermediate exploration diffusion (Exploration diffusivity section) can lead in a largely homogeneous space exploration. panels b), d) and Figure.4.
These examples show that search area restrictions and obstacles can have a significant impact on the spatial uniformity in random searches. These results indicate that specific environmental conditions may require the modification of the search strategy in order to satisfy certain spatial uniformity requirements.
Analyse Temporal Profile
We also did a review of the revisiting time profile as it evolved over time. It is important to remember that not all strategies are capable of providing a particular revisiting profile. Figures.4 and 5 don’t show this. Search problems that are subject to uncertainty and consider latency or movement may wish to favor homogeneous temporal reconsidering or to avoid revisiting at specific intervals. (see36). This analysis is shown at Fig.6 for Craters map, with a selection of four representative strategies, Ballistic random bounce and Lvy Mirror bounce. The second video animation (Supplementary Video 2), allows us to better illustrate temporal profile analysis by showing revisit intervals and their evolution over time.
Panel a) of Fig.6 shows a snapshot showing the temporal distribution for each exploration strategy at step300K. The colour blue indicates a recent visit, while red and brighter colours indicate longer delays. Different patterns signify different revisiting profiles of each search strategy. Searches with a uniform blue colour palette produce frequent revisits with different spatial patterns. This representation of distinct colour patches indicates a greater temporal heterogeneity. Brownian Search is an example of this heterogeneity. Although it can provide uniform spatial coverage (Supplementary Video 1) it is notably heterogeneous as regards to the time since the last visit.

Revisit time analysis. We will use the Craters map as an example. We will also examine four search strategies with different exploration diffusivity levels (see Figure.4). (A) A colour map representation of the time since last visit to each cell at step number 300K. This animation (Supplementary video 2) is also available. This representation shows the non-uniformity in the Brownian strategy. Markers 1 through 3 denote the locations of three cells, which will be discussed later. During a 100M step simulation, the revisit sequence was also saved for each cell. (b) Cumulative distribution function (CDF) of the revisit intervals for every cell. There are three overlayed tracks that correspond to the CDFs for cells 1 and 2. The ballistic strategy shows significantly higher redundancy around the search area limits (cell 3) (c) Revisit sequence for cell 2 on a plot where each data point is the revisit interval annotated at the corresponding simulation time step. It is the only strategy that has revisit times and has heterogeneous revisiting. (>10^5)These lines are indicated by a vertical line and translate into empty horizontal stripes. This effect can be overcome by using a short-term memory (Brownian memory) to reduce local repetitions. This memory has a similar temporal profile as the Lvymirror bounce strategy. The ballistic strategy has medium revisit times, with a concentration of between (10^3) (10^5).
Panel b) in Figure 6. shows the cumulative distribution function, (CDF), of cell revisit intervals for the same strategies as panel a and Supplementary Video 2. The revisit times were saved at each cell for each visit during the 100M-step simulation. The CDF for each grid cell was then computed. Each trace of CDF was then combined to create the shaded panels in the panel. Brighter traces indicate more frequent probability distributions. Three cells were chosen and their respective CDFs were highlighted in colour. Cell1 (red), located in the region between the craters (and the nearest search boundary), cell2 (blue), at an area away obstacles and bounds and cell3(green) is close to the search boundary away the craters. You can see the differences in the temporal profiles for the three representative cells. The step-like evolution seen in cell 3 (in contrast to cell 2, for the ballistic hunt) highlights the shorter revisit times close to the boundaries for this strategy.
Panel c in Figure 6. shows the sequences of revisit times for cell 2. Each data point corresponds to a revisit interval annotated during the occurring simulation step. This panel shows that the search area size, shape, and unpopulated revisit range are the most important factors in the ballistic strategy. (10^2)The cell-to-boundary distance defines the boundary. The Brownian strategy incorporates a local memory. This results in two distinct effects. (10^2)These are the ones that have been retold less often than those mentioned above. (10^5). This suggests that the temporal profile could be deliberately modulated using a local memory and its parameterised sizes to achieve a specific revisiting profile.
To optimize a random search strategy, it is possible to use the knowledge of target latencies and the effects of search parameters, intrinsic and extrinsic, on the revisit temporal profile. This work presents a novel way to analyse these strategies in terms of their spatial and temporal distribution. This method can be combined with diffusivity requirements, the distributions of search targets to satisfy the spatial- and temporal characteristics of a hunt under a specific problem or uncertainty level.
