[ad_1]
Australia’s catastrophic east coast floods have been described by the NSW premier as a “One in 1,000 years eventThis term has caused a lot of confusion.
Lengthy explanations that these terms are not the same as “occurring 1,000 years apart” or “once every 1,000 years” have only added to the confusion.
The simplest explanation is that the actual meaning of “one in 1,000 years” is “having a probability of 0.1 per cent in any given year” (1 in 1,000), which raises the question: why doen’t people simply say that?
The main reason is that these terms date back to a time when most people didn’t think in terms of probabilities, and even those who did were confused about how they worked. Nowadays, we all interact with probabilities.
The daily weather forecast also includes a PercentageProbability of rain and longer-term forecasts indicate the likelihood of more or less than average rainfall, according to El Nino/La Nina cycles.
Financial markets bet on the movements of interest rates or probabilities. Children learn statistics and probability in school.
However, this is a recent development.
Even the simplest concepts of probability theory weren’t known until the 17th Century. People considered fate and fortune to be essentially inexplicable. Even gamblers didn’t understand odds.
The birth of probability
It was indeed a Request from a friend or gamblerBlaise Pascal, a French philosopher and mathematician, was inspired in 1654 to develop the basic concepts for probability with Pierre de Fermat, a fellow mathematician.
(Pascal also used the idea to develop “Pascal’s wager” used to demonstrate the usefulness of believing in God. The idea is that believers will be rewarded with everlasting bliss if God exists. If they don’t believe in God, they will have to give up a few earthly pleasures while they are still alive. The benefit of believing that God exists, no matter how small, is infinite. However, the cost of not believing in God is finite.
Understanding developed slowly. It was not until the mid-18th century that English clergyman Thomas Bayes was credited with the field’s most important development.
Bayes bequeathed the tool
In its modern interpretation Bayes’ theoremIt allows us to revise our views on the likelihood of an event in light of the evidence from the past.
The recalculation includes updated assessments of the probability that something is relevant, as well as the explicit input of whether or not something has just occurred.
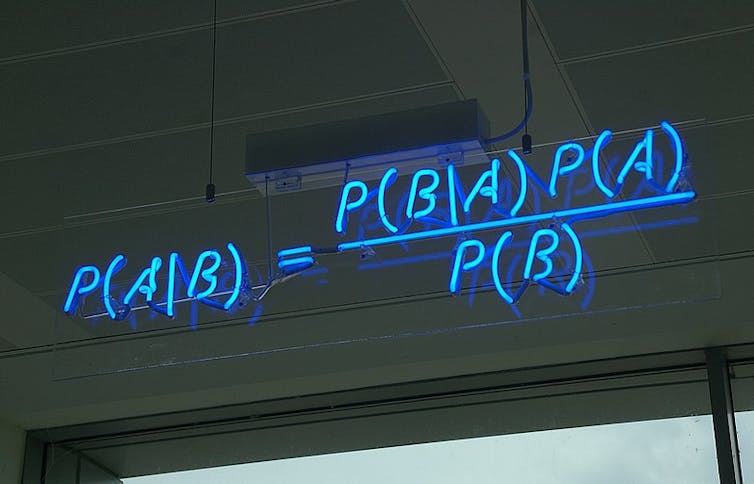
Wikimedia Commons, CC BY
Until Bayes, most probabilities were calculated as if they were unchanging, such as the probability of getting “heads” when tossing a coin. Those probabilities could usefully be described as “one in 1,000 years”, or “on average, every second toss”.
However, the likelihood of severe flooding changes with time as the relationships between the components of the weather system change. Evidence of this change can be found in the fact that floods have occurred.
This makes it no longer helpful to refer to a severe flood as “one in x years” event.
Continue reading:
Bayes’ Theorem is a maths tool that most of us use every day. But, what exactly is it?
It’s long past the time we changed the terminology of once-in-so-many years, but to what? The answer seems obvious, but the details will be complicated.
First, we need convert the old measures into severity levels, similar to those used to assess earthquakes and cyclones, but specific for each catchment.
This will allow you to calculate the probability of an event with a given severity.
What would happen if an event like the Lismore flood occurred?
Continue reading:
“One of the most severe disasters in colonial Australian History”: Climate scientists discuss the floods, and what the future holds
The initial “one in 1,000 year” description means that such an event would be extremely unlikely if the old relationship held.
Using Bayes’ theorem, we would update the initial one in 1,000 probability on the basis of updated information about the chance the underlying relationships are changing, producing new annual probabilities each year.
This is how it works Machine learningWorks and how medicalAnd InsuranceThese odds have been updated. The revised probabilities are almost certain to exceed one in 1,000.




