[ad_1]
This study, as mentioned above, aims at shedding light on the deep uncertainties associated climate change phenomenon. The seasonally-averaged surface air temperature, hereafter simply referred to as temperature, was selected as the non-conditional climatic variable to be monitored within the Karkheh River Basin, Iran, during the baseline period (1975–2005). Climate-change projections were made using the CORDEX datasets RCP 8.5.
The proposed framework begins by identifying the most appropriate theoretical distribution function to represent stochastic behavior patterns in historical and climate change data sets. These distributions were: lognormal, exponential and 3-parameter Weibull. Extreme value, gamma. Loglogistic. It is important that you note that the primary strategy of this study is to analyze data from a numeric perspective without any presumption regarding the stochastic nature of the data44. Therefore, the study would choose any distribution that is most appropriate to describe the data. Tables contain a summary of the fitting distributions to represent prior distributions and likelihood function. S1 to S4(See the Appendix). Furthermore, the climate-change period was divided into three mutually exclusive time frames which are short-term (2010–2039), mid-term (2040–2069), and long-term (2070–2099) future to gain a better understanding of the evoluton of future temperature changes.
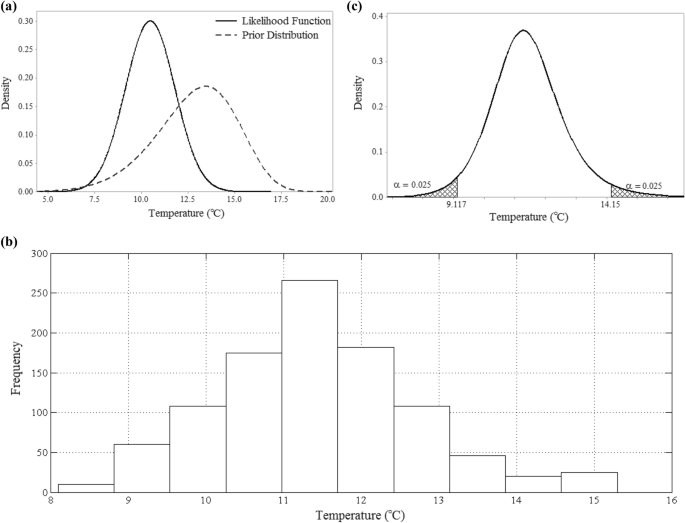
With Bayes’ theorem in mind, a Markov Chain Monte Carlo (MCMC) method was then applied to merge the prior distributions and the likelihood functions and to generate a sample set from the posterior distribution set. After a series if trials and errors, the sample size of the MCMC algorithm was finally determined to be 1000.n = 1000). These sample sets were then used for determining the most appropriate theoretical scenario. pdfs stands for posterior distribution functions. Figure 3For example, illustrates the most appropriate theoretical distribution to represent the posterior distribution of the Seimareh subbasin during spring in the short-term period.
The step-by-step procedure for computing the posterior pdf: (a)The distribution of Seimareh’s sub-basin during spring, and the likelihood function for this sub-basin in spring Short–term future; (b)The histogram of the generated samples; (c)The posterior distribution
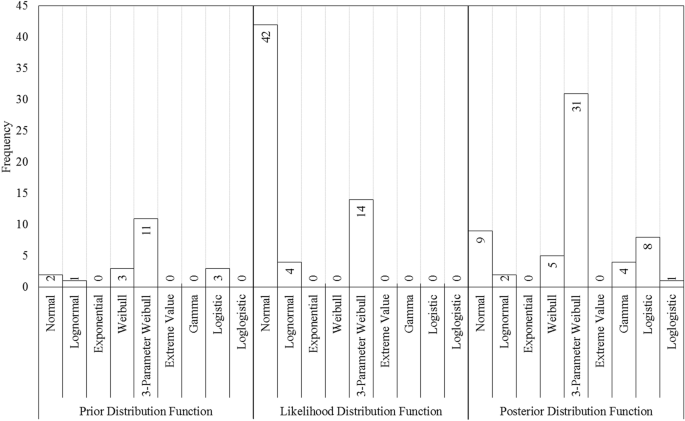
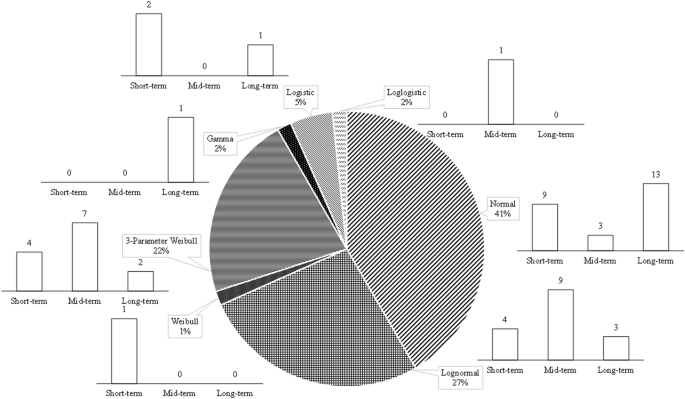
Figure 4This graph shows the frequency with which each of the specific theoretical distribution functions was deemed most appropriate to characterize the posterior, likelihood, or prior distributions. Analyzing the fitted pdfs in Fig. 4 reveals an important point about the nature of RCMs’ raw projections. The 3-parameter Weibull distribution function is the most popular for posterior and prior distributions. However, the normal distribution was more successful than any other available options in terms of likelihood functions. The type of selected theoretical distribution used for the prior and subsequent was also important. pdfs seems to be more diverse than those from the likelihood function. The likelihood functions only allowed for three types of distributions, and most of them are normal distributions. These functions are the most useful. pdfs that were aligned to the RCMs projected outcomes. The cause behind this notion might be traced back to the nature of RCMs’ projections. RCMs provide a more detailed and precise horizontal resolution than GCMs. This allows them to provide valuable information for management purposes. The data analysis revealed that the normal distribution, which was the most suitable distribution to describe the data 70% times, was the best. This could be interpreted as signaling that employing RCMs’ raw projections, especially for regions that have considerable volatility in their climatic variables, should be used with caution, and further adjustment to the raw projected data may be required in some cases. The normal distribution is not statistically significant and may not be the best way of presenting this data. The fact that, in most cases, it has been selected as the best way to portray the stochastic nature of the likelihood function (i.e., RCM’s projections) means that innate characteristics of these data might prevent them to truly represent these types of variables on their own.
The frequency with which each theoretical concept is used pdfs can be used to denote prior, likelihood function, or posterior distributions.
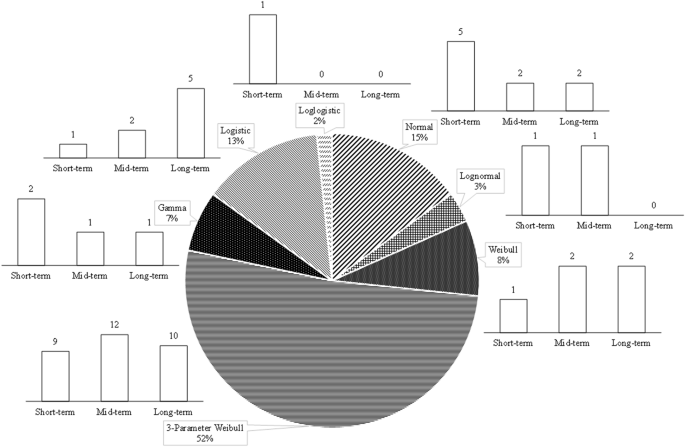
Figure 5Additional information is provided about the frequency at which each of these theoretical distributions was deemed appropriate to represent the posterior pdfs. While posterior sets are indeed the most varied in terms of the variety of distributions they contain, a significant number of fitted distributions exist. pdfHowever, s (approximately 52%) are fitted by a 3-parameter Weibull distribution. Additional information about the fitted distributions is available to represent the posterior pdfTables contain s S5 to S7 (Appendix).
The frequency with which different theoretical distributions are used as posterior pdfs.
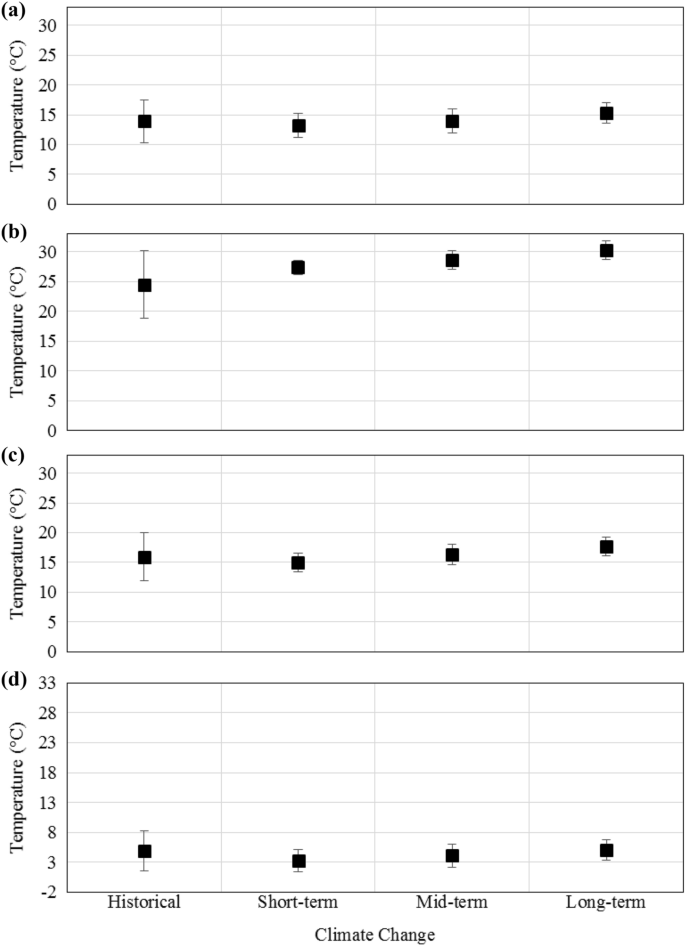
The computed posterior distribution function can be understood as modified representations, or stochastic behavior, of temperature variable with respect to short-term, medium-term, and longer-term climate change projections. Fig. shows the average temperature for the entire basin using a confidence interval of 95%. 6Climate change and historical conditions. There are two types of behavior patterns that have been observed. The first one is a broad summer trend. The second describes the rest. In summer (Fig. 6b) There is a steady, mildly positive trend (upward). The average temperature of the basin will increase with time. As for the rest, it appears that the average temperature in the basin would see a slight decrease in the short-term. However, the temperature would start to rise slowly with the passage of time. Spring (Fig. 6Fig. 6c. Time series. It is predicted that the expected average temperature of the basin will eventually surpass those experienced in the baseline condition in both the short-term and long term future. It is shown in Fig. 6It is expected to rise over time. However, it is possible that it will not reach the average temperature of the basin within the given time frames. Given the upward trend in data, this temperature could indeed be reached in a shorter timeframe. These patterns are consistent with the idea of earlier climate change impacts amplifying historical patterns in climatic variables. The data shows a slight decrease in the colder seasons and an increase in the warmer ones. This will continue until a new global climatic equilibrium is achieved. The temperature would then start to rise gradually as shown in the illustration.
The historical and simulated temperatures of the entire basin within the 95% confidence interval (a) spring; (b) summer; (c)Autumn; and (d) winter.
Another important implication can be understood by analysing Fig. 6The difference in the widths of the confidence intervals between baseline and climate change conditions. Comparable to the baseline conditions, the lengths of the 95% confidence intervals under climate change conditions would be dramatically reduced. This shrinking means that the generated results are more tightly surrounded by the central tend measure herein chosen for the meanμ) of the data. This notion is still in line with the idea that RCM’s projections mostly resemble the stochastic characteristic of normal distributions. Normal distributions are by nature not heavily-tailed, so they rarely produce tail values. Despite the fact that the MCMC framework has somewhat mitigated this effect, they still inherit this stochastic property via the likelihood functions.
To fully understand the results obtained here, it is important to first understand how Bayesian models work. Bayesian-based frameworks adjust the prior assumptions regarding a stochastic phenomenon using observed samples. In this example, the prior information is the historical data and the likelihood function (i.e. the samples) are obtained from RCM projects. As can be seen here, while RCMs’ projections might be perfectly capable of portraying the normal behavior of a variable under climate change conditions, which is usually sufficient for most lumped evaluation of climate change impact assessments, they might not be suitable to study extreme hydro-climatic events. The problem with raw RCM projections is their symmetric distribution. Figure 4This suggests that even though the MCMC framework is reducing the impact, the final projections inherit this property through the likelihood functions. This means that any RCM-based projection can be used to understand the overall impact of climate change. However, they are not the best choice to study extreme events. pdfThey rarely produce truly extreme values. Table summarizes the average temperatures in all subbasins for climate change and baseline conditions. 1.
It is evident that the data on the impact of climate changes are associated with deep uncertainty. This means that the parameters that describe the stochastic behavior and variability of a variable could be subject to some degree uncertainty. These parameters can be used to predict the impact of climate change. μ for one, may also be represented by a pdfThey are their own. This study focuses specifically on the deep uncertainty that could interfere with the central tend measure. μ.
The deep uncertainty in this instance dictates that the recorded parameters for each posterior distribution are not deterministic values. The MCMC would produce a particular type of posterior for a given prior distribution. pdfThe parameters used to define this pdf (e.g., μ), could vary each time the algorithm is used. If this variation is mild, there is more certainty about the nature of the variable’s stochastic behavior pattern (i.e., the posterior distribution function). If it is determined that the parameters are experiencing severe variations then the deep uncertain environment would leave the decision-makers unsure about the variables’ stochastic behavior pattern.
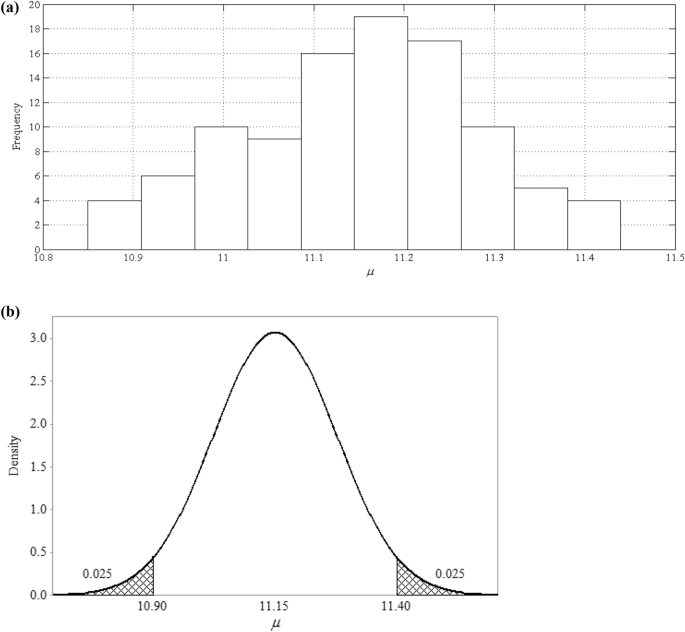
With this idea in mind, the combination of likelihood functions and prior distributions was run 100 times. In each iteration, the mean of 1000 samples were recorded. The recorded values were then fitted with a theoretical distribution function. The parameters of the computed posterior are then applied if the recorded numbers are close numerically. pdfs are less vulnerable to deep uncertainty. However, if these values show significant fluctuations, then the deep uncertainty of climate changes would make it difficult to predict the stochastic pattern of temperature. Figure 7For example, a depicts the uncertainty of the computed μ parameter for Seimareh sub-basin in spring under short-term future condition.
The uncertainty of the calculated μ parameter for Seimareh sub-basin in spring under short-term future condition demonstrated by (a)A histogram and (b)A probability distribution function.
Figure 8The number of times each theory distribution was chosen to depict the stochastic behaviour of the μ parameter. As you can see, the lognormal and normal distributions are the most common. pdfThe term s is used to describe the variation in μ parameter. Notable is also the fact that approximately 65% are normal distributions when describing the future condition. The fitted list pdfTables summarize s S8 to S10.
The frequency with which each distribution was found to be suitable for describing the stochastic distribution μ parameter.
Table 2The computed variation is summarized below μ parameter in each given sub-basin. It can be seen in Table 2The confidence interval of 95% μ parameter in all cases ranges between ± 0.1 and ± 0.3 °C. In 55% of the cases, this interval was found not to be more than ± 0.1 °C, and, furthermore, in 97% of them the interval was less than ± 0.2 °C. It is obvious that the confidence interval for the has been widened. μ parameter can only signal that the deep uncertainty has a more pronounced impact on the temperature’s stochastic behavior. As for the case of the spring data set of the Seimareh sub-basin under the short-term condition, or the case of the Gharesou sub-basin’s winter data series under short-term period, the confidence interval for the μ parameter is estimated to be ± 0.3 °C wide. This is a significant difference from other projected posteriors. pdfThere is less certainty about the expected stochastic behavior pattern for temperature variables in these cases. As shown in Table 2In some cases, the projections may differ from the actual. μ temperature’ posterior pdfs is decreasing in time (for a particular season over different timeframes). This was explained earlier as the deep uncertainties in climate change projections. Lower volatility indicates that the variable is less affected the climate-change phenomenon. This observation is consistent with the belief that the climate change phenomenon will intensify the historical patterns of climatic variables in the near future. However, we expect to see a gradual upward trend in temperature over the longer term.45. In this instance, volatility is higher in the earlier time frames. However this volatility seems to decrease as time passes. This means that the projected projections show less uncertainty about the overall behavior of the parameter in the long-term future, as models that simulate the climatic behavior under climate changes conditions have already reached an equilibrium.
